《张朝阳的物理课》介绍量子力学(2)

因此，只需要求出所有的ψ_E即可得到一般的波函数。ψ_E满足的方程为

波函数的物理意义是什么呢？假如利用薛定谔方程求解得到波函数，能做出什么物理预言呢？这就涉及到量子力学的诠释了。目前物理学界的主要观点是统计诠释，波函数的模方等于测量粒子位置时测量结果的概率分布。因此，波函数需要满足归一化条件：波函数模方在全空间的积分等于1，代表的是在全空间内找到粒子的概率为1。可归一化是一个很强的条件，很多量子化的来源都是波函数的可归一性质。“波函数是一个单值的、处处连续的、可归一化函数”，总结成简单的口诀，就是波函数“单值、连续、可归一”

在其后的互动环节中，张朝阳还与现场听众探讨了各种物理问题。比如“在低能级的时候，系统的能量是离散的，但是能量高的时候，系统的能量表现为连续的，这是为什么呢？”为了解答这个问题，张朝阳以氢原子能级举例说明。氢原子的能量正比于-1/n^2，当氢原子处于低能级的时候，n很小，能量表现为离散的。当氢原子处于高能级时，n很大，虽然这时能量依然是离散的，但是能级之间的间隔趋于无穷小，因此能量表现为连续的。

那么

这些数学概念都太抽象了，因此张朝阳以简单的三维空间为例来说明波函数空间的性质。在三维空间中，任何矢量都可以在直角坐标系的基矢下展开，比如位置矢量：

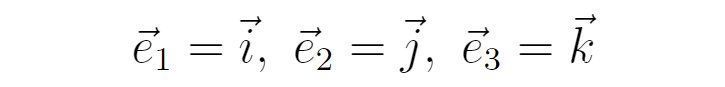
受普朗克的启发，爱因斯坦进一步假设光是一种粒子，并以此解释光电效应。光电效应指的是光照射到金属上“打”出了电子，并形成电流。根据经典理论，光电效应的出现是由于电磁波的电场部分使电子在金属中运动并逃逸出来。由此，即使光的频率比较低，只要光足够强，就可以出现光电效应。然而实验表明，存在一个截止频率，当电磁波的频率低于截止频率时，无论光强多大，都无法产生光电流。而爱因斯坦利用光子的概念成功地解释了光电效应。

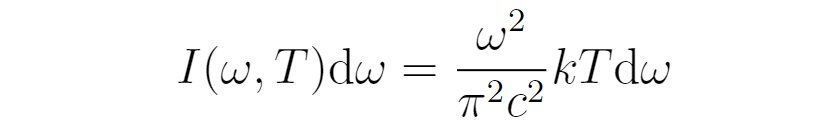
它被称为定态薛定谔方程。满足定态薛定谔方程的态被称为能量本征态，它具有固定的能量E，且能量值是哈密顿算符的本征值。

对于双原子分子气体，它有3个平动自由度，2个转动自由度，以及2个振动自由度，根据能量均分原理，单个分子的平均能量应该等于7kT/2，于是双原子分子气体的绝热指数为9/7。但是在室温下，双原子分子气体绝热指数的实验值约为1.4，经典理论值与实验值存在明显偏离。若考虑量子效应，双原子分子的固有频率很高，而谐振子能级间隔正比于固有频率，从而室温下振动自由度没有被激发，此时能量均分原理不适用于振动自由度。考虑这一点之后，双原子分子的平均能量为5kT/2，由此可以得到绝热指数为7/5=1.4，与实验值相符。

介绍完三维空间的情况，就可以对波函数空间作出类似的表述了。把波函数空间内的函数看成矢量，它们有和三维空间类似的“点乘”，更正式地，应该表述为内积，具体形式如下：

此外，中国科学院物理研究所副研究员李治林作为特邀嘉宾，与张朝阳一起和听众们进行了互动交流。“如果使用很大的力挤压氢原子会发生什么？”李老师对这个问题进行了解答。在量子力学里，比“力”更方便的是“势”及其梯度的概念，因此，所谓用很大的力挤压氢原子，可以等效描述为逐渐变窄的、陡峭的势阱对氢原子的约束。考虑无限深势阱，当势阱宽度逐渐变窄时，氢原子的动量不确定度越来越高，能量也越来越高。如果是一维无限深势阱，那么氢原子还会从其他方向逃逸出来。如果是三维无限深势阱，随着“挤压”过程的继续，在最极端的情况下，甚至氢原子自身也会发生改变，其中的质子和电子会通过弱相互作用形成一个中子并释放出一个中微子。这与中子星的形成机制是类似的。

就表示测量动量后，与得到的动量值相对应的概率密度。因此，前面使用的动量均值公式是合理的。

张朝阳介绍说，他在这里讲的量子力学是波动力学。在量子力学诞生初期，有两种形式的理论被提出来，一种是波动力学形式，另一种是矩阵力学形式，不过后来这两种形式被证明是等价的。

文章来源：《应用力学学报》 网址: http://www.yylxxb.cn/zonghexinwen/2022/0512/916.html