《张朝阳的物理课》介绍量子力学

观察上式，可以定义动量算符，形式如下：

对于不同的E，会得到不一样的f(t)，以及不一样的波函数空间部分。因此，对波函数添加下标E以示区别。从而原来的波函数可写为

回忆前面介绍的统计诠释，它可以拓展到沿任意一组本征矢的展开式上，其中展开系数的模方就表示系统在测量后处于相应本征态的概率(密度)。比如

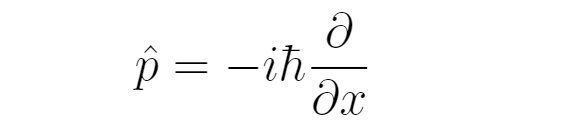
这个算符对应经典力学的哈密顿量，因此又被称为哈密顿算符。考虑了势能之后，薛定谔方程为

这样得到的黑体辐射谱为

经典物理的危机 波粒二象性

经典波动方程的其中一部分解可以写为f(x-vt)，对比上式的形式，可以知道光速c=ω/k。因此，光子的动量还可以改写为

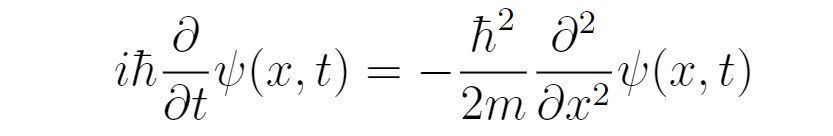
其中δ_{ij}被定义为

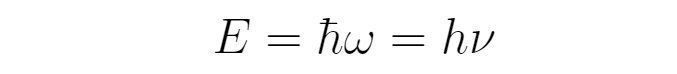
动量算符在一个具体的态ψ(x)下的均值为

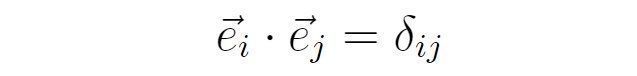
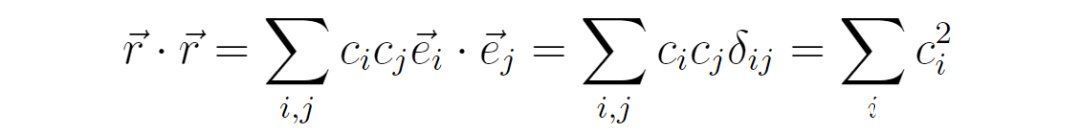
所以

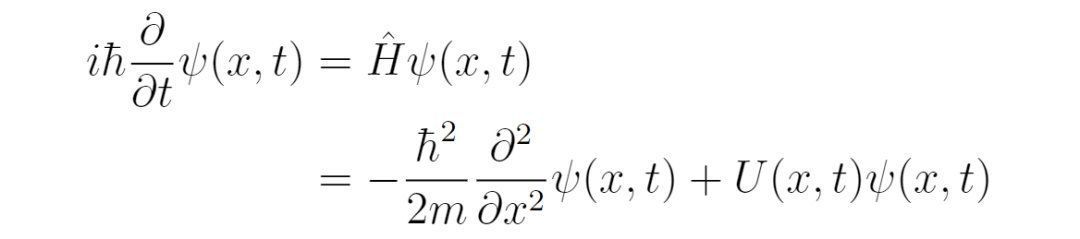
其中h上加一横是约化普朗克常数，等于h/(2π)，h是普朗克常数。如果电子掉进了原子核里，由于原子核的尺度很小，从而电子的位置不确定度很小，相应的动量的不确定度很大，于是电子的动量在很大概率上能够使得电子逃离原子核的束缚。从这个角度讲，量子力学的不确定性原理确保了原子核的稳定性。

所以

本次线下课，张朝阳开门见山地先介绍起了量子力学。张朝阳介绍，量子力学对宇宙中物质结构的形成意义非凡。根据经典物理，电子绕着原子核旋转，就像太阳系中行星绕着地球旋转一样；由于电子带有电荷，它做圆周运动时具有加速度，从而会辐射电磁波，导致原子的总能量不断降低，电子最终会坠入原子核。但是现实中的原子是稳定的，这与经典物理的预言相差很大。要对这一切作出解释，就必须要用到量子力学。在量子力学里，位置和动量是不能同时精确测量的，这就是不确定性原理。位置和动量的不确定度满足

如果考虑存在势场U(x,t)的情况，那么粒子的总能量就要包含势能。为此，引入如下能量算符：

其中*号表示对波函数求复共轭。波函数空间上也存在相应的单位正交基。特别地，每一个经典物理量对应的算符的全部本征矢在归一化之后可以构成一组单位正交基(注：严格的表述是，自共轭算符的全部本征矢在归一化后构成一组完备正交基。诸如能量、动量、角动量、位置这四个常用的物理量对应的算符都是自共轭算符)。比如，对于动量算符，它的本征矢满足

为了理解上式的含义，可以将ψ(x)在动量本征矢下的展开式代入，有

爱因斯坦假设的光子能量与普朗克假设的黑体辐射单份能量一致。假设光子(动)质量为m，由狭义相对论，光子能量为E=mc^2，动量p=mc，那么动量可以改写为

假如本征矢已经归一化，那么

可以用另一组符号来表示这一组基矢：

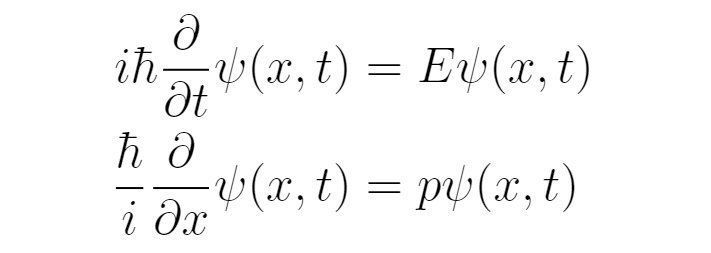
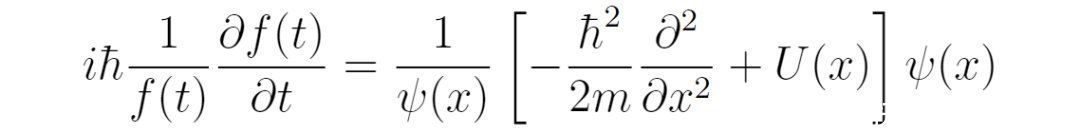
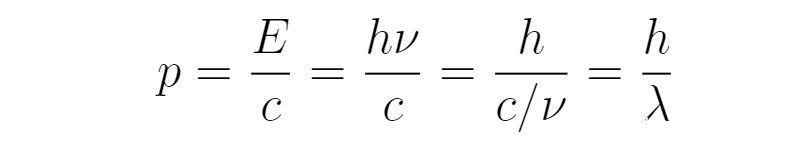
它在红外端(低频部分)与实验结果接近，但在紫外端(高频部分)是发散的，与实验不符。经典黑体辐射的紫外发散被称为“紫外灾难”。为了解决“紫外灾难”，普朗克假设黑体辐射的能量是一份一份的，且每一份的能量为

于是

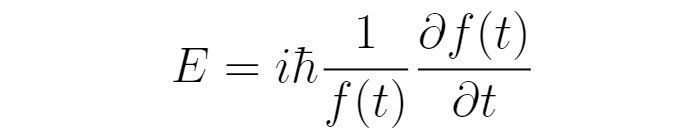
当势能不随时间改变时，可以借助分离变量法去掉波函数对时间的依赖。假设波函数的空间部分和时间部分可以分离：

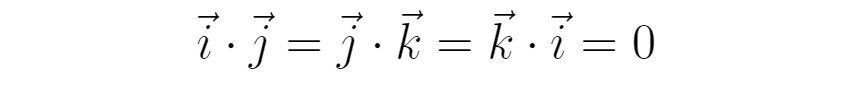
这个公式与实验结果符合得非常好。

互动环节中，有听众还提到了与往期课程中潮汐相关的问题，例如：潮汐的周期为什么不是精确的12小时？张朝阳解释说，如果月球静止不动，那么潮汐的周期确实是半天，也就是12小时。但是在地球自转的同时，月球也在绕着地球公转，公转方向和地球自转方向一致。考虑到这一点之后，可以计算出潮汐的周期比12小时长大约二十多分钟。

借着能量标度的概念，张朝阳介绍说元素周期表是化学周期表，对应的是化学过程。虽然同位素的中子数不一样，但是因为带有相同数量的质子，导致核外电子结构几乎一致。化学反应主要由核外电子决定，所以同位素的化学性质几乎一样。但是在物理上，同位素对应的原子不是同一种粒子，它们的物理性质可能差别很大。比如，对比放射性元素铀-235和铀-238，在核裂变和链式反应方面，两者差别明显，一般用铀-235作为核反应的原料。

文章来源：《应用力学学报》 网址: http://www.yylxxb.cn/zonghexinwen/2022/0512/916.html